En matemáticas, el coseno es una función par y continua con periodo , y además una función trascendente. Su nombre se abrevia cos.
En trigonometría, el coseno de un ángulo de un triángulo rectángulo se define como la razón entre el catetoadyacente a dicho ángulo y la hipotenusa:
Esta razón no depende del tamaño del triángulo rectángulo escogido sino que es una función dependiente del ángulo
Si pertenece a la circunferencia goniométrica, es decir, la circunferencia de radio uno con se tiene:
Ya que .
Esta construcción permite representar el valor del coseno para ángulos no agudos y funciona exactamente igual para los vectores, representando un vector mediante su descomposición en los vectores ortogormales y .
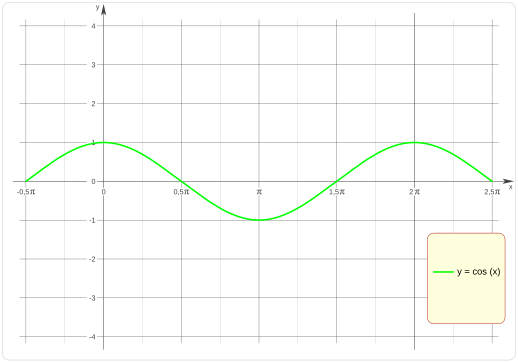
Representación gráfica del coseno
Valores del Coseno:
- 0º → cos 0 = 1
- 30º → cos 30 = √3 / 2
- 45º → cos 45 = √2 / 2
- 60º → cos 60 = 1/2
- 90º → cos 90 = 0
- 180º → cos 180 = -1
- 270º → cos 270 = 0
- Relación del coseno con el seno:
sen² α + cos² α + = 1
cos α = sen (α + π/2)
- Coseno de la suma de ángulos:
cos (α+ β) = cos α cos β - sen α sen β
- Coseno de la resta de ángulos:
cos (α - β) = cos α cos β + sen α sen β
- Coseno de la ángulos suplementarios:
cos (π - α) = - cos α
Coseno del ángulo opuesto:
cos (2π - α) = cos α
- Coseno del ángulo negativo:
cos (- α) = cos α
Características
fundamentales de la función coseno son las
siguientes:
1)
Su dominio es R y es continua.2) Su recorrido es [- 1, 1] ya que - 1 ≤ cos x ≤ 1 .
3) Corta al eje X en los puntos π/2 + k·π con k∈Z .
Corta al eje Y en el
punto (0, 1) .
4)
Es par, es decir, simétrica respecto al eye Y.
cos (x) = cos
(- x)
5) Es
estrictamente creciente en los intervalos de la forma (a,
b) donde
a= - π + 2·k·π y b = 0 + 2·k·π siendo k∈Z .
Es estrictamente decreciente en los intervalos
de la forma(a, b) donde
a = 0 + 2·k·π y b = π + 2·k·π siendo k∈Z .
6)
Tiene infinitos máximos relativos en los puntos de la
forma (2·k·π,1) con k∈Z .
Tiene infinitos mínimos relativos en los
puntos de la forma (π
+ 2·k·π, - 1) con k∈Z .
7)
Es periódica de periodo 2π .cos (x) = cos (x + 2π)
La función f(x) = cos (k·x) es periódica de periodo p = 2π/k
Para |k|>1 el periodo disminuye y para 0< |k| <1 el periodo aumenta.
8) Está acotada superiormente por 1 e inferiormente por - 1.
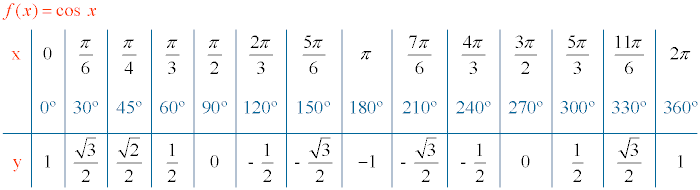

















No hay comentarios:
Publicar un comentario