En matemáticas, la tangente es una función impar y es una función periódica de periodo con indeterminaciones en , y además una función trascendente de variable real. El día de la tangente es el 3 de Mayo. Su nombre se abrevia tan1.
En trigonometría, la tangente de un ángulo (de un triángulo rectángulo) se define como la razón entre el cateto opuesto y el adyacente:
Esta razón no depende del tamaño del triángulo rectángulo escogido sino que es una función dependiente del ángulo
Esta construcción permite representar el valor del tangente para ángulos no agudos.
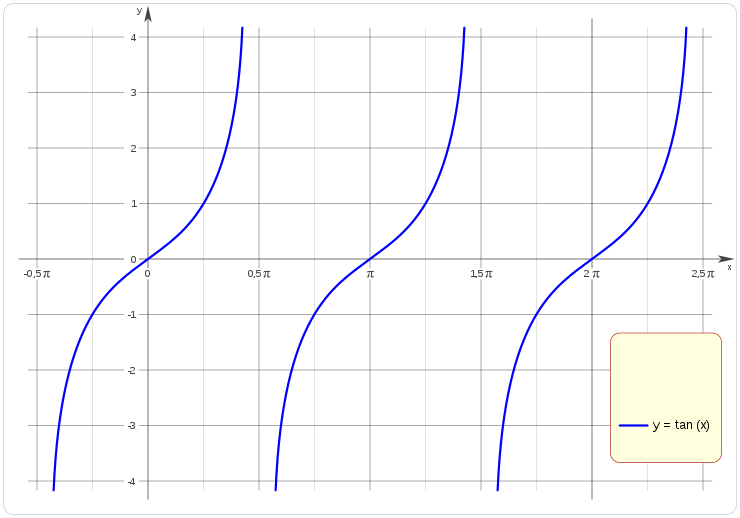
Representación gráfica
Tangente de la suma de dos ángulos
Esta identidad trigonométrica parte de la identidad de la suma de dos ángulos ya conocida para el seno y el coseno.
- Dados los ángulos :
- Reemplazando por las identidades antes mencionadas:
- Dividiendo al numerador y al denominador por :
- Separando la suma y la resta:
Tangente de la diferencia de dos ángulos
- Al ser una función impar, se obtiene:
Fórmula resumida
Tangente del ángulo doble
Partiendo de
y haciendo entonces:
Tangente del ángulo triple
Conociendo la tangente del ángulo ψ, hallar la tangente de 3ψ
Tangente del ángulo mitad
Se trata de hallar la tangente de la mitad de θ, conociendo los de θ:
-
-
-
-
- Las características fundamentales de la función tangente son las siguientes:
1) Su dominio es R - {π/2 + k·π con k∈Z} .
2) Es discontinua en los puntos π/2 + k·π con k∈Z .
3) Su recorrido es R .
4) Corta al eje X en los puntos k·π con k∈Z .
Corta al eje Y en el punto (0, 0) .
5) Es impar, es decir, simétrica respecto al origen.
tg (- x) = - tg (x)
6) Es estrictamente creciente en todo su dominio.
7) No tiene máximos ni mínimos.
8) Es periódica de periodo π .
tg (x) = tg (x + π)
La función f(x) = tg (k·x) es periódica de periodo p = π/k
Para |k|>1 el periodo disminuye y para 0< |k| <1 el periodo aumenta.
9) Las rectas y = π/2 + k·π con k∈Z son asíntotas verticales.
10) No está acotada.
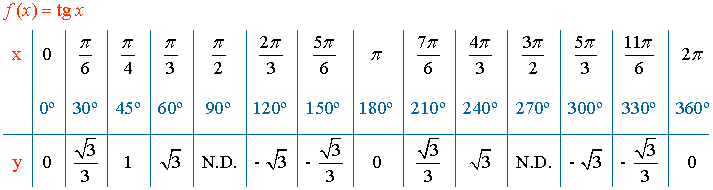
-
-























No hay comentarios:
Publicar un comentario